基数排序

简介

基数排序（英语：Radix sort）是一种非比较型的排序算法，最早用于解决卡片排序的问题。

它的工作原理是将待排序的元素拆分为个关键字（比较两个元素时，先比较第一关键字，如果相同再比较第二关键字……），然后先对第关键字进行稳定排序，再对第关键字进行稳定排序，再对第关键字进行稳定排序……最后对第一关键字进行稳定排序，这样就完成了对整个待排序序列的稳定排序。

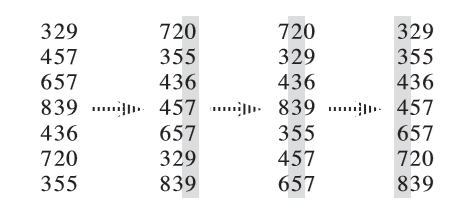
基数排序需要借助一种 稳定算法 完成内层对关键字的排序。

通常而言，基数排序比基于比较的排序算法（比如快速排序）要快。但由于需要额外的内存空间，因此当内存空间稀缺时，原地置换算法（比如快速排序）或许是个更好的选择。1

基数排序的正确性可以参考《算法导论（第三版）》第 8.3-3 题的解法或自行理解。

性质

稳定性

基数排序是一种稳定的排序算法。

时间复杂度

一般来说，如果每个关键字的值域都不大，就可以使用计数排序作为内层排序，此时的复杂度为，其中为第关键字的值域大小。如果关键字值域很大，就可以直接使用基于比较的排序而无需使用基数排序了。

空间复杂度¶

基数排序的空间复杂度为。

算法实现

基数排序 (zoom)

cpp

const int N = 100010;
const int W = 100010;
const int K = 100;

int n, w[K], k, cnt[W];

struct Element {
  int key[K];

  bool operator<(const Element& y) const {
    // 两个元素的比较流程
    for (int i = 1; i <= k; ++i) {
      if (key[i] == y.key[i]) continue;
      return key[i] < y.key[i];
    }
    return false;
  }
} a[N], b[N];

void counting_sort(int p) {
  memset(cnt, 0, sizeof(cnt));
  for (int i = 1; i <= n; ++i) ++cnt[a[i].key[p]];
  for (int i = 1; i <= w[p]; ++i) cnt[i] += cnt[i - 1];
  // 为保证排序的稳定性，此处循环i应从n到1
  // 即当两元素关键字的值相同时，原先排在后面的元素在排序后仍应排在后面
  for (int i = n; i >= 1; --i) b[cnt[a[i].key[p]]--] = a[i];
  memcpy(a, b, sizeof(a));
}

void radix_sort() {
  for (int i = k; i >= 1; --i) {
    // 借助计数排序完成对关键字的排序
    counting_sort(i);
  }
}

JS 实现

jsx

Array.prototype.radixSort = function () {
	let arr = this.slice(0);
	var len = arr.length;

	function getNumLength(num) {
		if (num === 0) return 1;

		let length = 0;
		while (num) {
			num = Math.floor(num / 10);
			length++;
		}

		return length;
	}

	function getMaxDigit(arr) {
		var max = arr[0];
		for (var i = 1; i < len; i++) {
			if (arr[i] > max) max = arr[i];
		}

		return getNumLength(max);
	}

	let mod = 10;
	let dev = 1;

	let maxDigit = getMaxDigit(arr);
	let counter = [];

	for (var i = 0; i < maxDigit; i++, mod *= 10, dev *= 10) {
		for (var j = 0; j < len; j++) {
			var bucket = parseInt((arr[j] % mod) / dev);

			if (!counter[bucket]) counter[bucket] = [];
			counter[bucket].push(arr[j]);
		}

		var pos = 0;
		for (var j = 0; j < counter.length; j++) {
			var value = null;
			if (counter[j]) {
				while ((value = counter[j].shift()) != null) {
					arr[pos++] = value;
				}
			}
		}
	}

	return arr;
};

var a = [
	3, 5, 3, 0, 8, 6, 1, 22, 8, 33, 21, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9,
	7, 4, 0, 2, 6,
];

console.log(a.radixSort());

基数排序 ​

简介 ​

性质 ​

稳定性 ​

时间复杂度 ​

空间复杂度¶ ​

算法实现 ​

JS 实现 ​

基数排序

简介

性质

稳定性

时间复杂度

空间复杂度¶

算法实现

JS 实现