深色模式
BM31 对称的二叉树
描述
给定一棵二叉树,判断其是否是自身的镜像(即:是否对称)
例如下面这棵二叉树是对称的 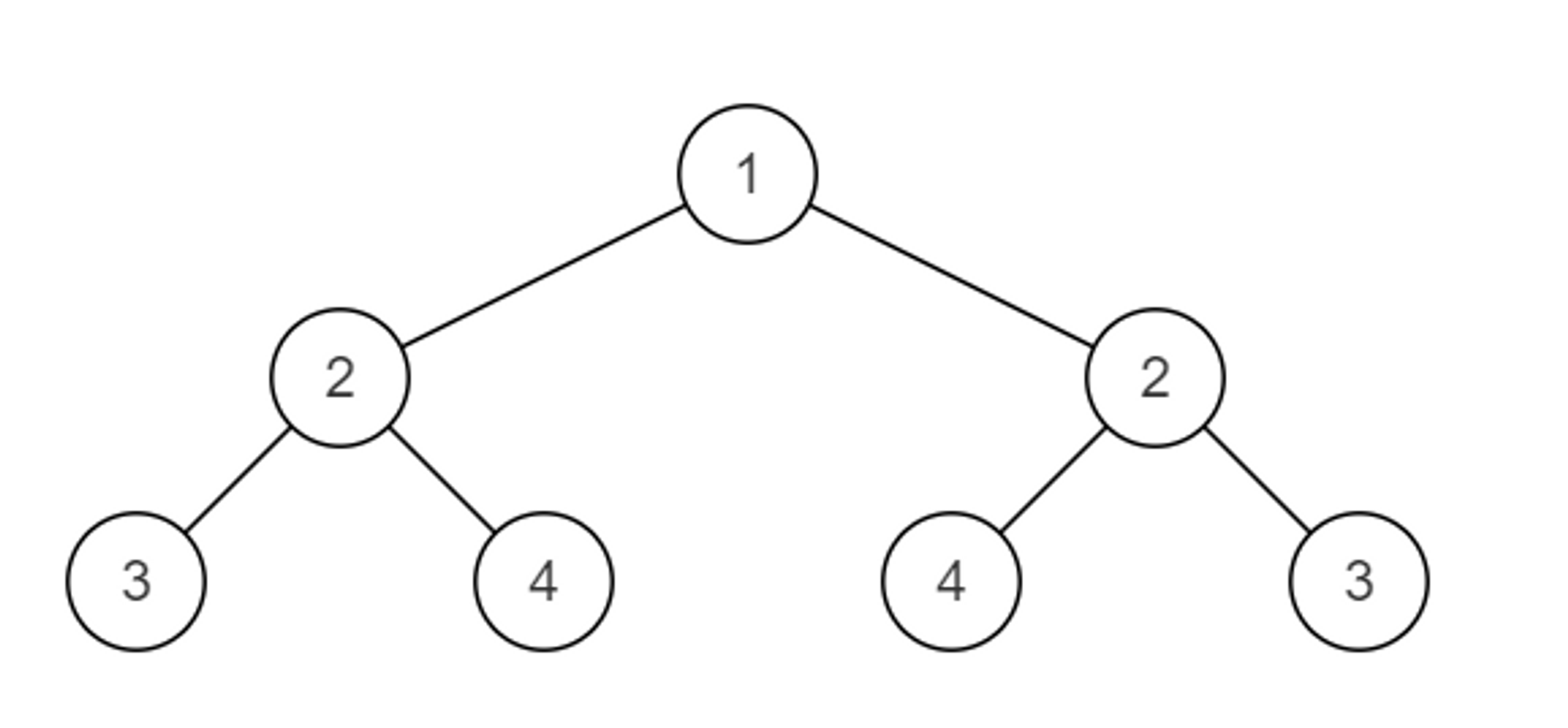
下面这棵二叉树不对称。 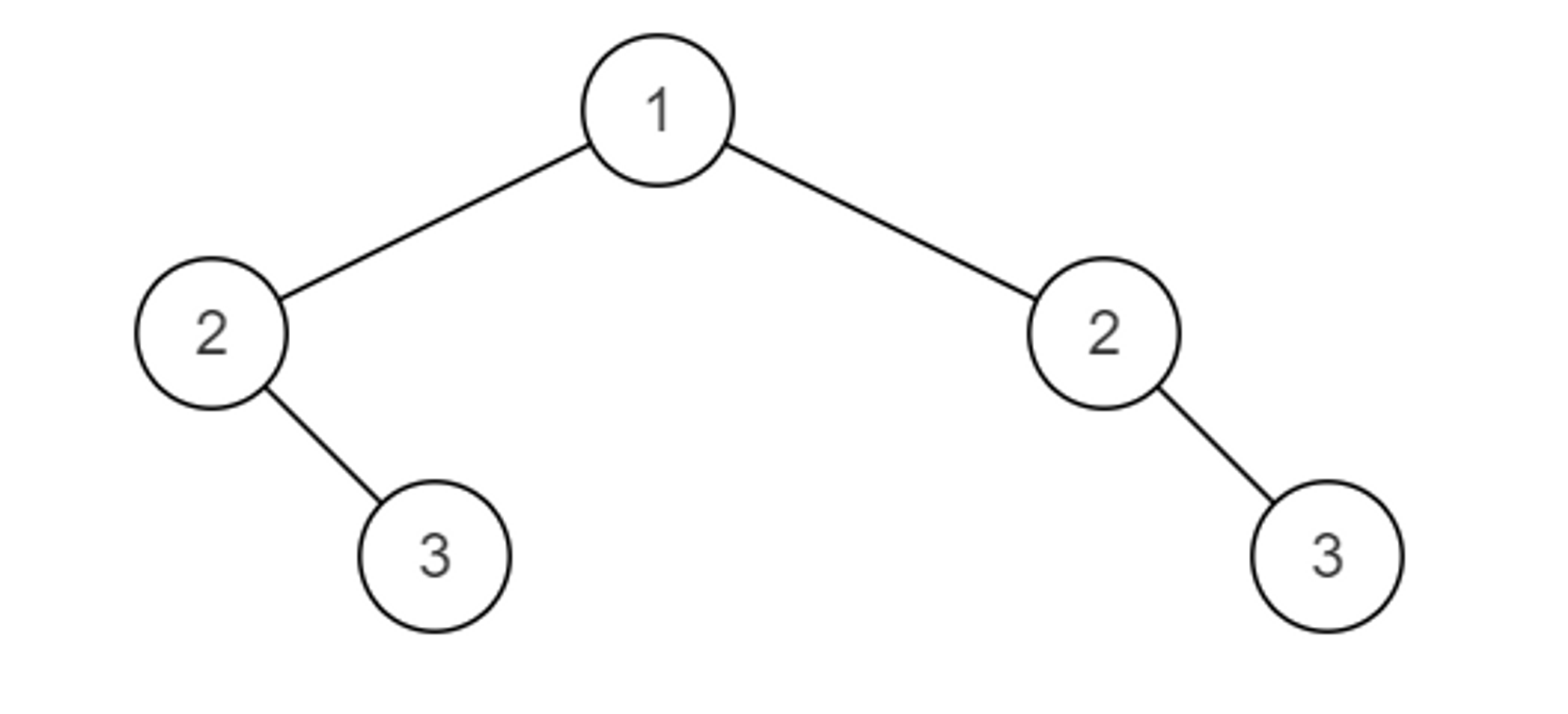
数据范围:节点数满足 10000≤n≤1000,节点上的值满足 |1000∣val∣≤1000
要求:空间复杂度 O(n),时间复杂度 O(n)
备注:
你可以用递归和迭代两种方法解决这个问题
示例1
输入{1,2,2,3,4,4,3}
返回值:true
示例2
输入:{8,6,9,5,7,7,5}
返回值:false
题解
tsx
/*class TreeNode {
* val: number
* left: TreeNode | null
* right: TreeNode | null
* constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.left = (left===undefined ? null : left)
* this.right = (right===undefined ? null : right)
* }
* }
*/
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
* @param pRoot TreeNode类
* @return bool布尔型
*/
export function isSymmetrical(pRoot: TreeNode): boolean {
// write code here
if(!pRoot) return true;
// 左右节点不对称
if((!pRoot.left && pRoot.right) || (pRoot.left && !pRoot.right)) return false;
if(!pRoot.left && !pRoot.right) return true;
var pstack: TreeNode[] = [pRoot.left];
var qstack: TreeNode[] = [pRoot.right];
while(pstack.length && qstack.length) {
var p: TreeNode = pstack.pop();
var q: TreeNode = qstack.pop();
if(!p || !q || p.val !== q.val) return false;
if((!p.left && q.right) || (p.left && !q.right)) return false;
if((!p.right && q.left) || (p.right && !q.left)) return false;
if(p.right && q.left) {
pstack.push(p.right);
qstack.push(q.left)
}
if(p.left && q.right) {
pstack.push(p.left);
qstack.push(q.right)
}
}
if(pstack.length || qstack.length) return false;
return true;
}递归
ts
public class Solution {
boolean recursion(TreeNode root1, TreeNode root2){
//可以两个都为空
if(root1 == null && root2 == null)
return true;
//只有一个为空或者节点值不同,必定不对称
if(root1 == null || root2 == null || root1.val != root2.val)
return false;
//每层对应的节点进入递归比较
return recursion(root1.left, root2.right) && recursion(root1.right, root2.left);
}
boolean isSymmetrical(TreeNode pRoot) {
return recursion(pRoot, pRoot);
}
}