树形选择排序

树形选择排序又称为锦标赛排序

思想

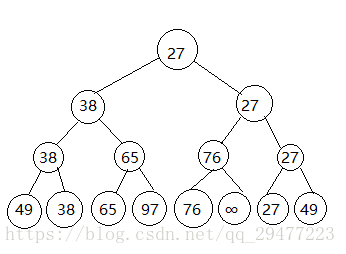
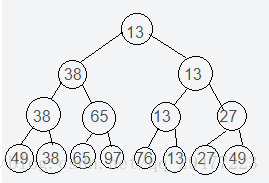
算法思想：树形选择排序也称作锦标赛排序。基本思想是先把待排序的n个记录的关键字两两比较，取出较小者，然后再在[n/2]个较小者中，采用同样的方法进行比较，选出每两个中的较小者，如此反复，直至选出最小关键字记录为止。这个过程可以用一棵满二叉树来表示，不满时用关键字为∞的节点填满，选择的最小关键字记录就是这棵树的根节点。在输出最小关键字之后，为选出次小关键字，将最小关键字记录所对应的叶子结点的关键字值置为∞，然后从该叶节点开始和其兄弟结点的关键字比较，修改从该叶结点到根结点路径上各结点的值，则根结点的值即为次小关键字。重复进行上述过程，直到所有的记录全部输出为止，如图所示给出了选取最小及次小关键字的过程。

树形选择排序1 树形选择排序2

代码

Array.prototype.treeSelectSort = function () {
	let arr = this.slice(0);
	var len = arr.length;
	var tree = []; // 完全二叉树结构
	var treeSize = 2 * len - 1;
	var low = 0;

	// 将数组数据复制到 tree数组中，叶子节点
	for (var i = len - 1, j = 0; i >= 0; i--, j++)
		tree[treeSize - 1 - j] = arr[i];

	// 填充非叶子节点
	for (var i = treeSize - 1; i > 0; i -= 2)
		tree[Math.floor((i - 1) / 2)] =
			tree[i - 1] < tree[i] ? tree[i - 1] : tree[i];

	var minIndex;

	while (low < len) {
		min = tree[0];
		arr[low++] = min;
		// 查找minIndex
		minIndex = treeSize - 1;

		while (tree[minIndex] !== min) minIndex--;
		// 查找到叶子节点中的minIndex 将其数据设置成∞，表示当前数据在当前一轮比较重已经选择出了最小的
		tree[minIndex] = Infinity;

		// 调整其父节点最小数据
		while (minIndex) {
			// 如果是右节点
			if (minIndex % 2 === 0) {
				tree[Math.floor((minIndex - 1) / 2)] =
					tree[minIndex - 1] < tree[minIndex]
						? tree[minIndex - 1]
						: tree[minIndex];
				minIndex = Math.floor((minIndex - 1) / 2);
			} else {
				// 是左节点
				tree[Math.floor(minIndex / 2)] =
					tree[minIndex] < tree[minIndex + 1]
						? tree[minIndex]
						: tree[minIndex + 1];
				minIndex = Math.floor(minIndex / 2);
			}
		}
	}

	return arr;
};

var a = [
	3, 5, 3, 0, 8, 6, 1, 22, 8, 33, 21, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9,
	7, 4, 0, 2, 6,
];

console.log(a.treeSelectSort());

树形选择排序 ​

思想 ​

代码 ​

树形选择排序

思想

代码