深色模式
BM7 链表中环的入口结点
参考BM6
ts
/*class ListNode {
* val: number
* next: ListNode | null
* constructor(val?: number, next?: ListNode | null) {
* this.val = (val===undefined ? 0 : val)
* this.next = (next===undefined ? null : next)
* }
* }
*/
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param pHead ListNode类
* @return ListNode类
*/
export function EntryNodeOfLoop(pHead: ListNode): ListNode {
// write code here
var fast: ListNode = pHead;
var slow: ListNode = pHead;
while(fast && fast.next) {
fast = fast.next.next;
slow = slow.next;
// 可以相遇
if(fast ===slow) {
// 重置fast 到 pHead
fast = pHead;
while(fast !== slow) {
fast = fast.next;
slow = slow.next;
}
return fast;
}
}
return null;
}为什么ptr和slow相遇的节点一定是入环点?
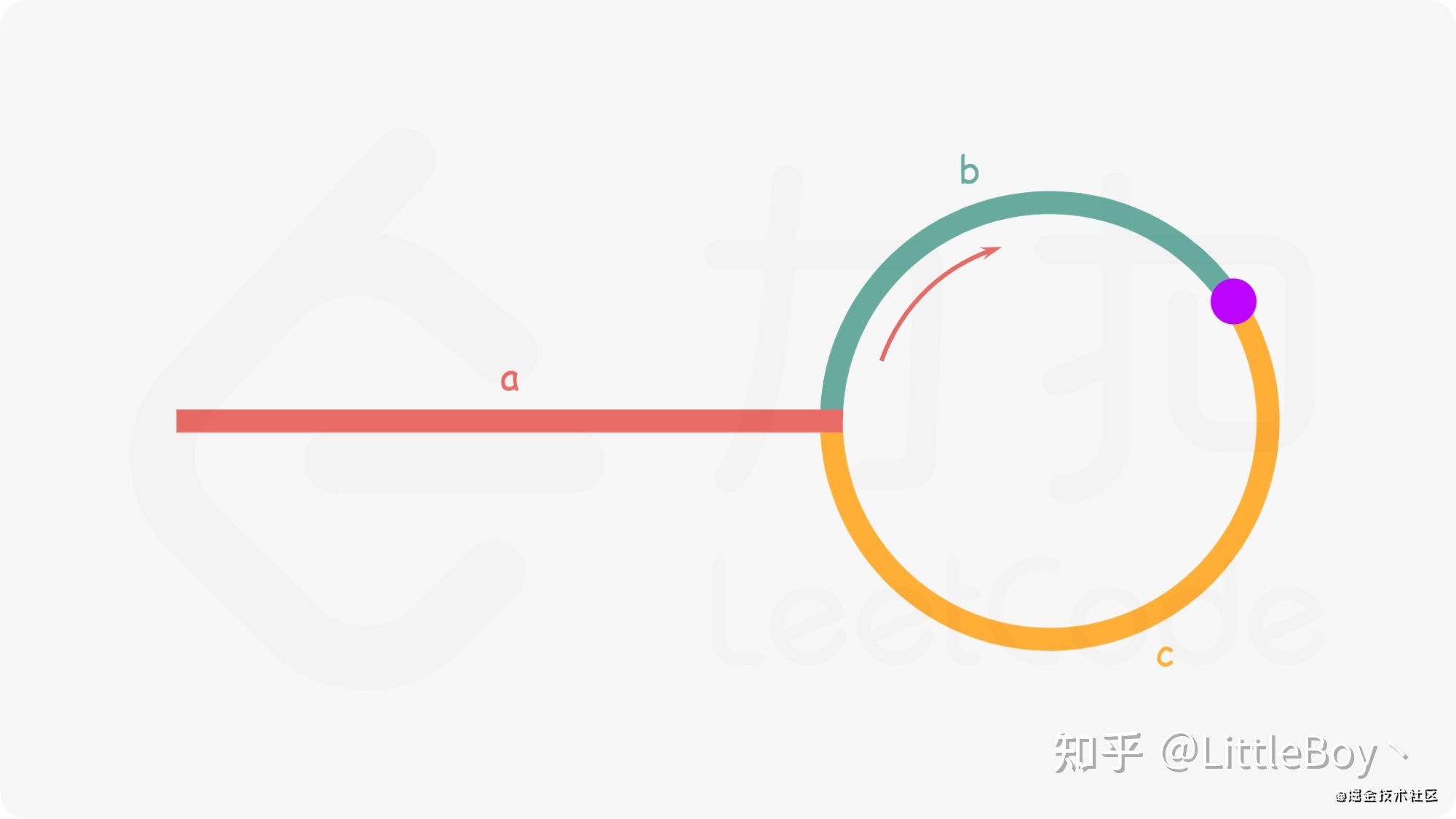
如图所示,假设环外部分长度为a,slow指针进入环后,又走了b的距离与fast相遇。此时,fast指针已经走完了环的n圈,因此它走过的总距离为: a+n(b+c)+b=a+(n+1)b+nc
任意时刻,fast指针走过的距离都为slow指针的2倍,而且由问题2的解答,我们已经知道,slow指针是不可能绕环超过一圈的,即相遇时,flow走的距离为a+b。因此得出关系式:
a=c+(n−1)(b+c)这个等量关系特别重要,其中c表示slow与fast指针相遇位置到入环点的距离,而(n−1)(b+c)则是 n-1圈的环长。
因此,只需要再添加一个指针指向头结点,当它走完环外距离a的时候,则会与在绕圈等它的slow相遇。而相遇点恰好是入环点。
