BM25 二叉树的后序遍历

1. 递归法

/*class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */
/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 
 * @param root TreeNode类 
 * @return int整型一维数组
 */

function postOrder(root: TreeNode, res: number[]) {
    if(!root) return res;
    if(root.left) postOrder(root.left, res);
    if(root.right) postOrder(root.right, res);
    res.push(root.val)
}
export function postorderTraversal(root: TreeNode): number[] {
    // write code here
    var res: number[] = [];
    postOrder(root, res);
    return res;
}

堆栈法

既然二叉树的前序遍历和中序遍历都可以使用栈来代替递归，那后序遍历是否也可以呢？答案是可以的，但是会比前二者复杂一点点。

根据后序遍历“左右中”的顺序，那么后序遍历也与中序遍历类似，要先找到每棵子树的最左端节点：

//该节点再次入栈
s.push(node);
//先访问右边
root = node->right;

然后我们就要访问该节点了嘛？不不不，如果它还有一个右节点呢？根据“左右根”的原则，我还要先访问右子树。我们只能说它是最左端的节点，它左边为空，但是右边不一定，因此这个节点必须被看成是这棵最小的子树的根。要怎么访问根节点呢？

我们都知道从栈中弹出根节点，一定是左节点已经被访问过了，因为左节点是子问题，访问完了才回到父问题，那么我们还必须要确保右边也已经被访问过了。如果右边为空，那肯定不用去了，如果右边不为空，那我们肯定优先进入右边，此时再将根节点加入栈中，等待右边的子树结束。

//该节点再次入栈
s.push(node);
//先访问右边
root = node->right;

不过，当右边被访问了，又回到了根，我们的根怎么知道右边被访问了呢？用一个前序指针pre标记一下，每个根节点只对它的右节点需要标记，而每个右节点自己本身就是一个根节点，因此每次访问根节点的时候，我们可以用pre标记为该节点，回到上一个根节点时，检查一下，如果pre确实是它的右子节点，哦那正好，刚刚已经访问过了，我现在可以安心访问这个根了。

//如果该元素的右边没有或是已经访问过
if(node->right == NULL || node->right == pre){ 
    //访问中间的节点
    res.push_back(node->val); 
    //且记录为访问过了
    pre = node; 
}

具体做法：

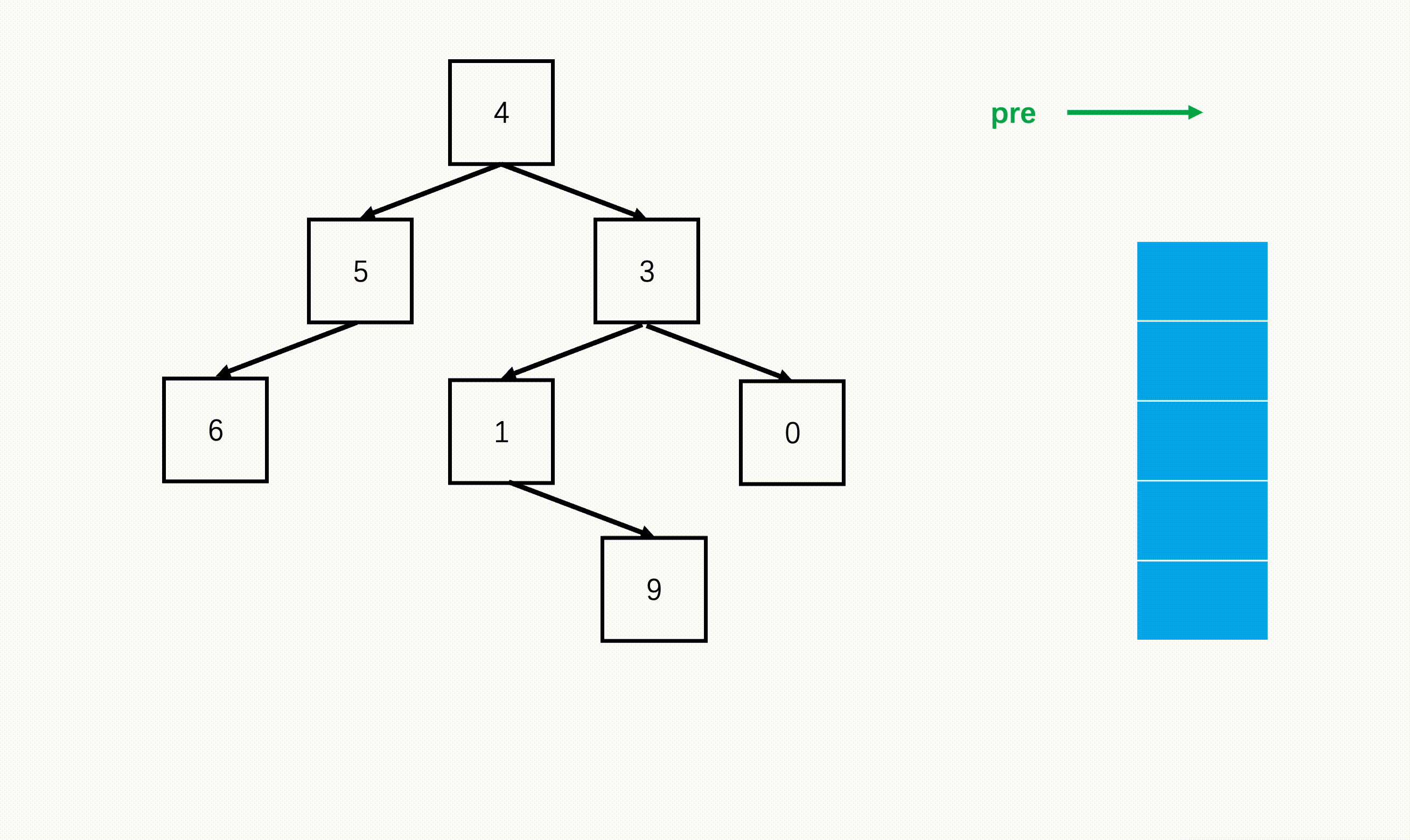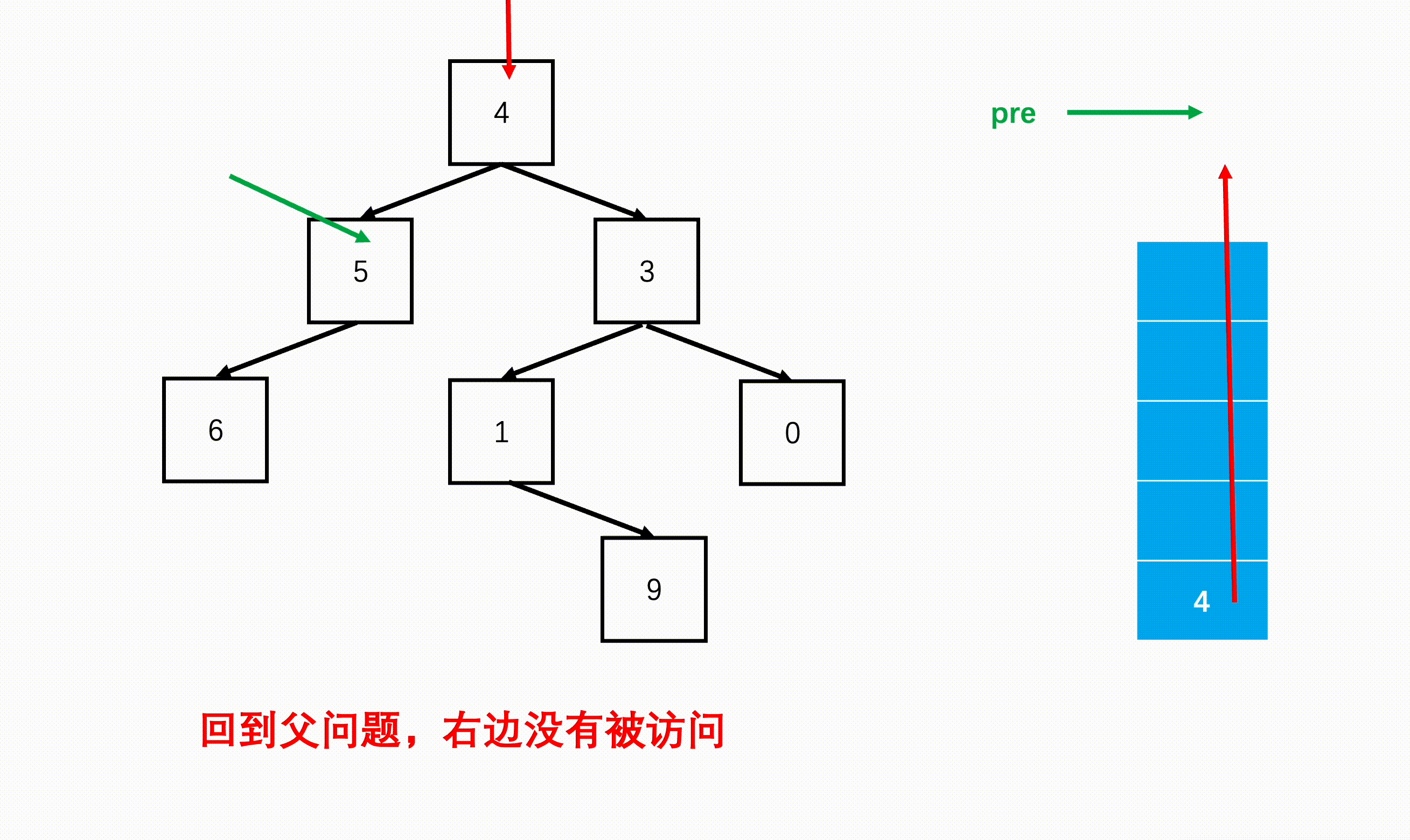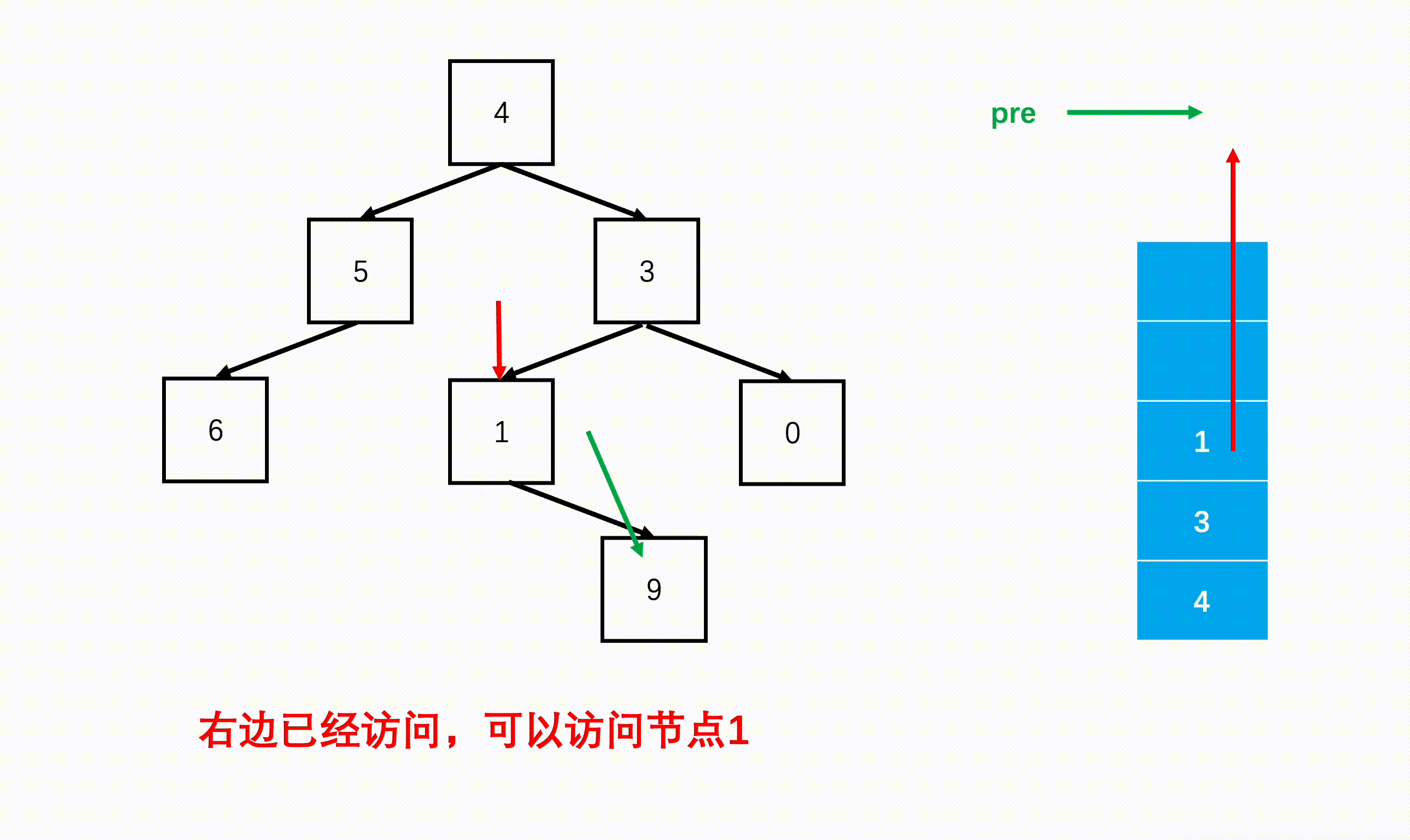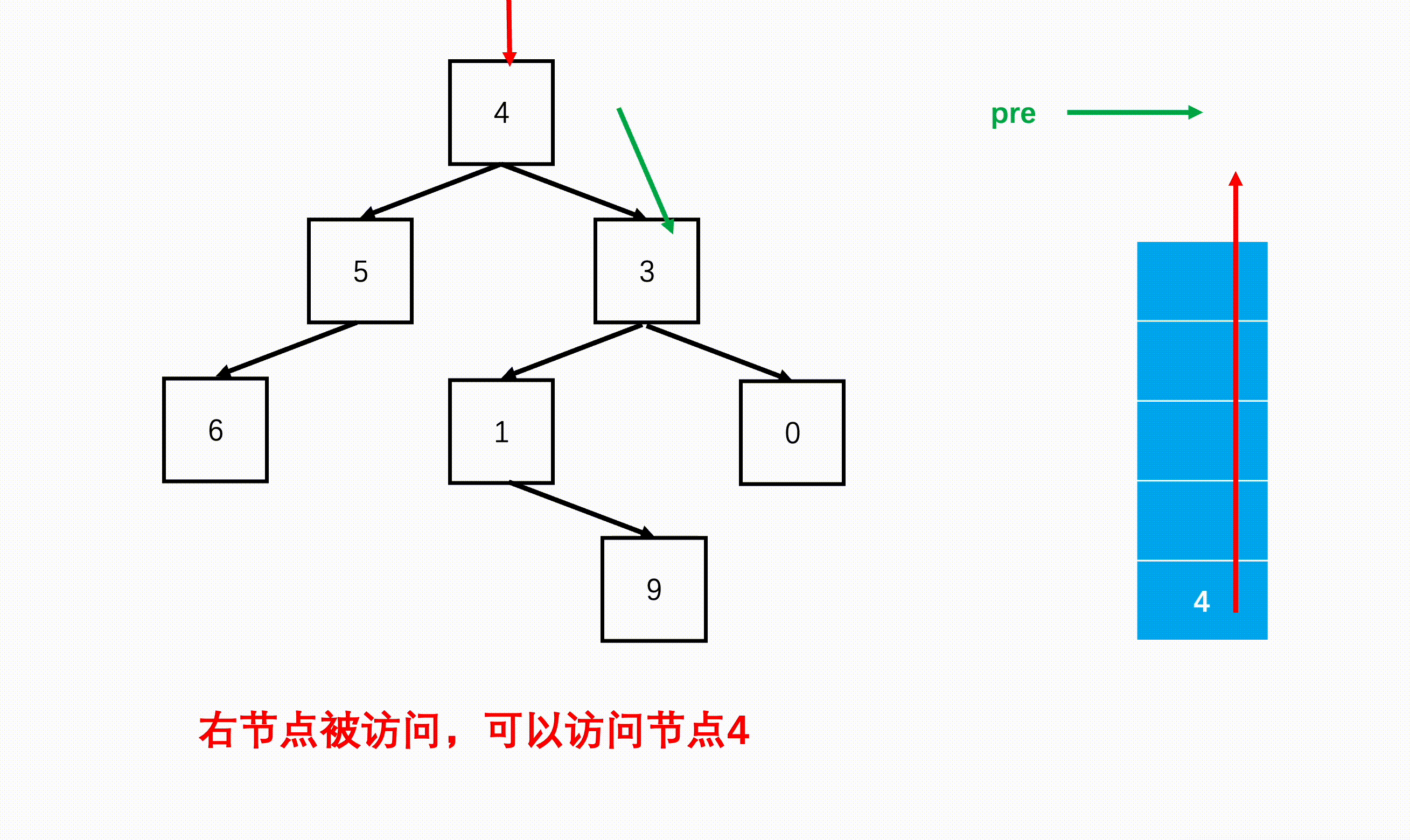
step 1：开辟一个辅助栈，用于记录要访问的子节点，开辟一个前序指针pre。
step 2：从根节点开始，每次优先进入每棵的子树的最左边一个节点，我们将其不断加入栈中，用来保存父问题。
step 3：弹出一个栈元素，看成该子树的根，判断这个根的右边有没有节点或是有没有被访问过，如果没有右节点或是被访问过了，可以访问这个根，并将前序节点标记为这个根。
step 4：如果没有被访问，那这个根必须入栈，进入右子树继续访问，只有右子树结束了回到这里才能继续访问根。

/*class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

/**
 * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
 *
 * 
 * @param root TreeNode类 
 * @return int整型一维数组
 */


export function postorderTraversal(root: TreeNode): number[] {
    // write code here
    var res: number[] = [];
    var stack: TreeNode[] = [];
    var pre: TreeNode;
    
    while(root || stack.length) {
        while(root) {
            stack.push(root)
            root = root.left;
        }
        var node = stack.pop();
//         如果该节点右节点不存在或右节点已经访问过了
        if(!node.right || node.right === pre) {
            res.push(node.val);
            pre = node;
        } else {
//             当前节点入栈
            stack.push(node);
            root = node.right;
        }
    }
    return res;
}

BM25 二叉树的后序遍历 ​

1. 递归法 ​

BM25 二叉树的后序遍历

1. 递归法