深色模式
堆排序
堆是什么
堆是一种二叉树树形结构,跟一把的数的却别是不需要额外存储保存指针关系。
堆分为大顶堆和小顶堆
大顶堆:父节点值大于子节点的值 小顶堆:父节点值小于子节点值
节点位置
通常堆以数组形式存储堆中的数据,假设一个节点的位置索引是 i , 数组起始位置为 0
- 左子节点所在位置
- 右子节点所在位置
- 父节点所在位置
堆的操作
在堆中最大值或最小值(优先队列)总是位于根节点。最大堆的操作有如下几种操作:
- 最大堆调整(Max Heapify):将堆的末端子节点调整,使得子节点永远小于父节点
- 创建最大堆(Build Max Heap):将堆中的数据重新排序
- 堆排序(Heap Sort):移除根节点,并做最大堆调整递归运算。
堆的应用
1. 最大的 K 个数和最小的 K 个数
最大的 K 个数: 大顶堆获取数据 最小的 K 个数:小顶堆获取数据
2. 排序算法
升序:小顶堆排序 倒叙:大顶堆排序
TIP
注意这个跟最大的 k 和最小的 k 个数使用相反,因为排序算法会交换顶点和末尾节点(不一定是数组最后一个)。
建堆过程
以大顶堆为例
- 从数组中最后一个非叶子节点开始向上调整。最后一个非叶子节点位置
,左子节点所在位置 ,右子节点所在位置 - 假设处理某个非叶子子节点,其后的非叶子子节点已排序好了。比较当前节点与其子节点大小关系。
- 如果当前节点比所有子节点大,则处理下一个非叶子子节点
- 如果当前节点小于子节点数值,则取子节点中最大值与当前节点交换, 记录最大子节点位置为
childIndex。向下处理子节点是否满足堆结构,当前节点i=childIndex,处理子节点。
画个图理解下,以 [3,5,3,0,8,6,1,5,8] 为例:
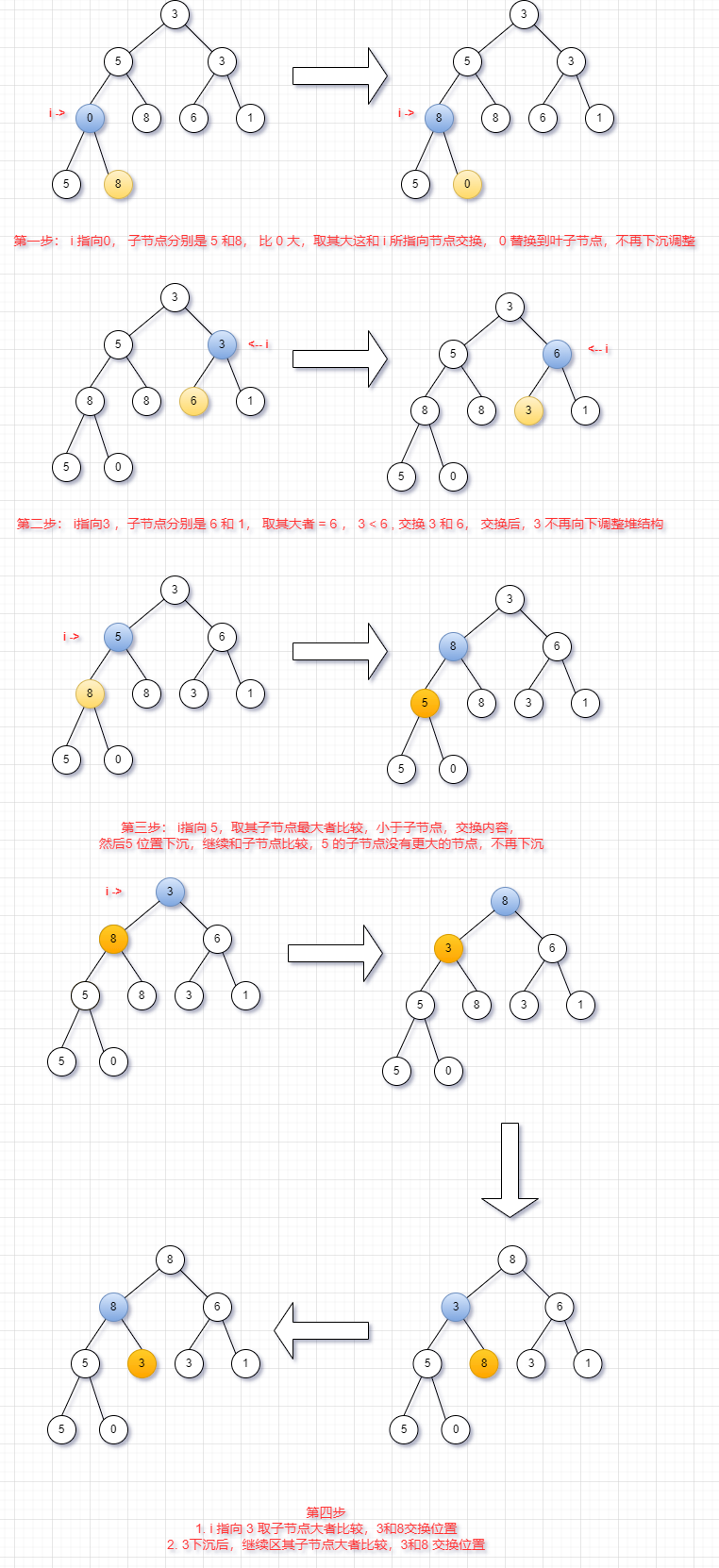
堆排序过程
- 建堆
- 取出堆顶节点,将待处理数组最后一个节点和堆顶节点交换,调整堆结构
- 待处理节点数目-1,循环执行 步骤 2 和 3 直到处理完毕
JS 算法
js
Array.prototype.heapSort = function () {
let arr = this.slice(0);
let len = arr.length;
function swap(i, j) {
let temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
// 类似 shiftDown
function maxHeapAdjust(start, end) {
let parent = start;
// 左节点
let child = start * 2 + 1;
// 子节点在下表范围类才比较
while (child <= end) {
// 先比较两个子节点中最大的
if (child + 1 <= end && arr[child] < arr[child + 1]) child++;
// 如果父节点比子节点大,则跳出循环,不再处理
if (arr[parent] > arr[child]) return;
// 否则,交换父子节点内容,子节点再和孙子节点比较
swap(parent, child);
parent = child;
child = child * 2 + 1;
}
}
// 初始化堆, 类似 buildHeap
for (var i = Math.floor(arr.length / 2) - 1; i >= 0; i--) {
maxHeapAdjust(i, arr.length - 1);
}
// 排序
for (var i = len - 1; i > 0; i--) {
swap(0, i);
maxHeapAdjust(0, i - 1);
}
return arr;
};
var a = [3, 5, 3, 0, 8, 6, 1, 5, 8, 6, 2, 4, 9, 4, 7, 0, 1, 8, 9, 7, 3, 1, 2, 5, 9, 7, 4, 0, 2, 6];
console.log(a.heapSort());python 实现
py
# 大顶堆
class MaxHeap(object):
def __init__(self, nums):
self.nums = nums
self.buildMaxHeap()
def buildMaxHeap(self):
size = len(self.nums)
# 建堆
for i in range(size // 2 - 1, -1, -1):
self.heapify(size, i)
# 调整节点 i 是否满足对结构
def heapify(self, n, i):
largest = i
left = 2 * i + 1
right = 2 * i + 2
if left < n and self.nums[largest] < self.nums[left]:
largest = left
if right < n and self.nums[largest] < self.nums[right]:
largest = right
if largest != i:
self.nums[i], self.nums[largest] = self.nums[largest], self.nums[i]
# 上面节点下放,继续验证是否符合堆结构,调整结构
self.heapify(n, largest)
def sort(self):
size = len(self.nums)
# 排序
for i in range(size - 1, 0, -1):
self.nums[i], self.nums[0] = self.nums[0], self.nums[i]
self.heapify(i, 0)
def pop(self):
size = len(self.nums)
if size == 0:
return None
self.nums[0], self.nums[size -1] = self.nums[size - 1], self.nums[0]
val = self.nums.pop()
size -= 1
self.heapify(size, 0)
return val
def add(self, num):
self.nums.append(num)
size = len(self.nums)
self.shiftUp(size -1)
def shiftUp(self, i):
while i > 0:
parent = (i -1) // 2
if self.nums[parent] < self.nums[i]:
self.nums[parent], self.nums[i] = self.nums[i], self.nums[parent]
i = parent
else:
break
if __name__ == "__main__":
nums = [5,6,2,3,1,7,9,8,10,1,2]
maxHeap = MaxHeap(nums)
# maxHeap.sort()
print(maxHeap.nums)
# for i in range(len(maxHeap.nums)):
# val = maxHeap.pop()
# print(val, maxHeap.nums)
# val = maxHeap.pop()
# val = maxHeap.pop()
# print(val, maxHeap.nums)
maxHeap.add(22)
print(maxHeap.nums)
maxHeap.add(23)
print(maxHeap.nums)
maxHeap.add(12)
print(maxHeap.nums)
maxHeap.add(13)
print(maxHeap.nums)